 Haskell Hero
Haskell Hero
Interaktivní učebnice pro začínající Haskellisty
|
|
Užitečné funkce IidUnární funkce vracející argument v nezměněné podobě. Definice
id :: a -> a id x = x Příklad použití
id 5 ~> 5 id "ahoj" ~> "ahoj" (id even) 3 ~> even 3 ~> False Složitější příklad
comp :: Int -> (a -> a) -> a -> a comp 0 _ = id comp n f = f . comp (n-1) fVýraz comp n f x se vyhodnotí tak, že se na prvek x aplikuje n-krát funkce f. Funkce id zde funguje jako zastavující hodnota pro případ, že hodnota v prvním argumentu se zmenší na nulu.
comp 5 (+2) 10 ~>* ( (+2) . (+2) . (+2) . (+2) . (+2) . id ) 10Operátor (.) je rozebrán v posledním odstavci.
constBinární funkce vracející svůj první argument v nezměněné podobě. Definice
const :: a -> b -> a const x y = x Příklad použití
const 5 'q' ~> 5 const True (+8) ~> True (const div "ffuu") 10 3 ~> div 10 3 ~> 3 Doplňující info
Výraz
flipTernární funkce, která si bere jako argumenty:
Následně prohodí pořadí druhého a třetího argumentu a tyto argumenty nechá zpracovat funkcí Definice
flip :: (a -> b -> c) -> b -> a -> c flip f x y = f y x Příklad použití
flip (-) 3 5 ~> 5 - 3 ~> 2 flip const True "jj" ~> const "jj" True ~> "jj" Konstruktor n-tic
Příklad použití
(,) 5 True ~> (5, True)
(,,) "aAa" 5.0 False ~> ("aAa", 5.0, False)
fstFunkce, která z uspořádané dvojice vrátí její první složku. Definice
fst :: (a,b) -> a fst (x,_) = x Příklad použití
fst ("#&!",10.5) ~> "#&!"
sndFunkce, která z uspořádané dvojice vrátí její druhou složku. Definice
snd :: (a,b) -> b snd (_,y) = y Příklad použití
snd ("#&!",10.5) ~> 10.5
Složené funkce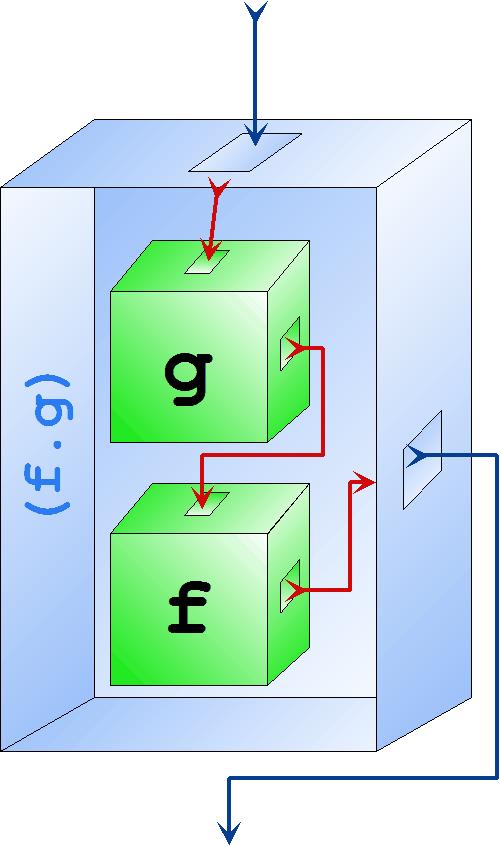 Krabičkové znázornění skládání funkcí
Ke skládání funkcí se používá ternární operátor
Argumenty operátoru
Výsledkem výpočtu je argument Definice
(.) :: (b -> c) -> (a -> b) -> a -> c (f . g) x = f (g x) Příklad
Definujte binární funkci
sndOdd ("ahoj",5) ~>* True
sndOdd (True,8) ~>* False
Do funkce vhodím dvojici čehokoli a celého čísla a vypadne z ní sndOdd :: (a,Integer) -> BoolJednou z možností by bylo použít definici podle vzoru: sndOdd (_,y) = odd yMy si zde ukážeme, jak tuto funkci definovat pomocí složené funkce. Chceme vytvořit funkci obecně znázorněnou modrou krabičkou na obrázku výše. Vhodíme do ní dvojici a vypadne z ní Bool.
Jako první si z uspořádané dvojice vytáhneme její druhou složku pomocí funkce snd (x,y)Poté na výsledek aplikujeme funkci odd:
odd (snd (x,y))Což můžeme napsat pomocí operátoru (.) jako složenou funkci. Výsledná definice bude tedy vypadat následovně:
sndOdd (x,y) = (odd.snd) (x,y)Pokud se nám podaří dostat argument funkce úplně doprava, můžeme jej ze zápisu vynechat. Takovému zápisu se říká pointfree. O převodu definice funkce do pointfree tvaru se budeme podrobně bavit později. Prozatím nám bude stačit vědět, že následující zápis je zaměnitelný s předchozím: sndOdd = odd.snd 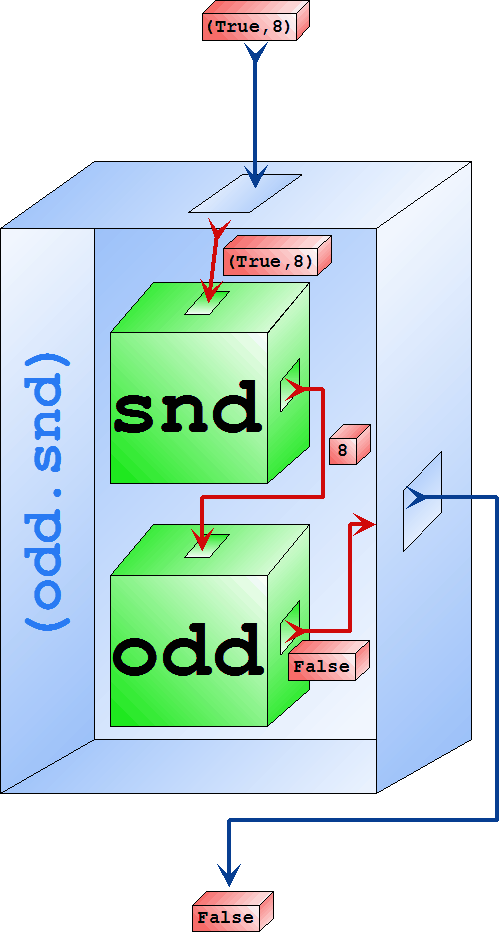 Vyhodnocení výrazu (odd.snd) (True,8)
|