 Haskell Hero
Haskell Hero
Interaktivní učebnice pro začínající Haskellisty
|
|
Typy IIIProč typové třídy?
Z předchozích lekcí o typech víme, že typ je krabička obsahující hodnoty se společnými vlastnostmi. Například
Jakého typu je funkce
Jak tedy Krabičky krabiček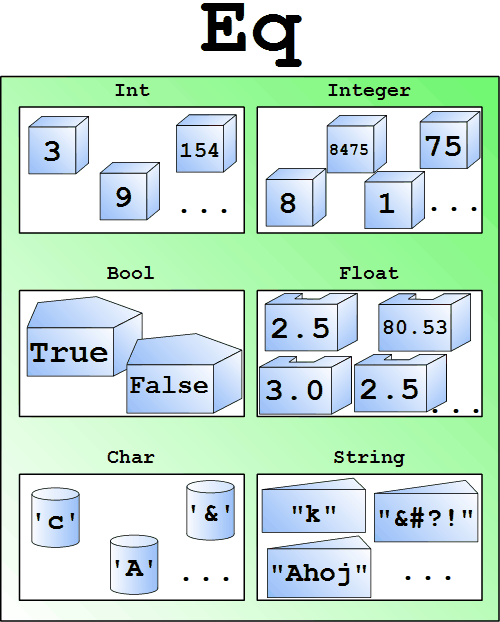 Znázornění typové třídy Eq
Tak toto je krabička (==) :: Eq a => a -> a -> BoolZnamená to funkce (==) může dostat dva argumenty jakéhokoli typu, který je z typové třídy Eq.
Jakého typu je funkce 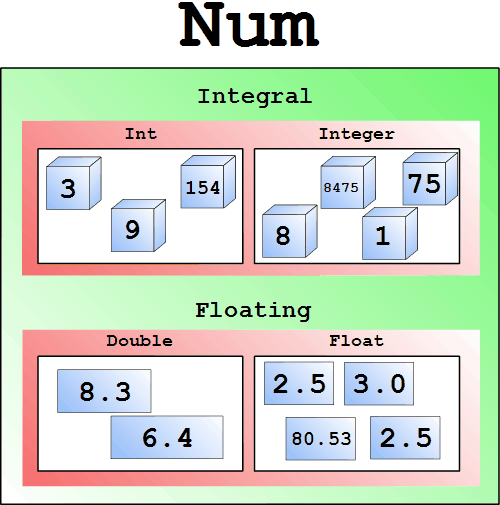 Znázornění typové třídy Num
Typ funkce (+) :: Num a => a -> a -> aTřída Num zahrnuje mimo jiné i podtřídy Integral, což jsou všechna celá čísla, a Floating, což jsou všechna desetinná čísla. Nám bude stačit, když budeme znát krabičku Num.
Ještě zbývá zmínit krabičku
Operátory (<) :: Ord a => a -> a -> Bool Vkládáme krabičky do krabičekNyní už víme, že existují funkce, které si jako argumenty berou "cokoli, co se dá testovat na rovnost". Například funkce zipWith (==) :: Eq a => [a] -> [a] -> [Bool]si bere dva seznamy čehokoli porovnatelného a vrací seznam pravdivostních hodnot. My bychom chtěli tuto funkci aplikovat například na dva seznamy typu [Nat], což jsou přirozená čísla, která jsme si definovali dříve. Jsou definována následovně:
data Nat = Zero | Succ NatChtěli bychom, aby bylo možné provést následující vyhodnocení výrazu: zipWith (==) [Zero, Succ Zero] [Zero, Succ (Succ Zero)] ~>* [True, False]Takové vyhodnocení ale není možné, protože Nat nepatří do třídy Eq. Co s tím? Vložíme typ Nat do třídy Eq. Provedeme to tak, že zadefinujeme rovnost dvou hodnot typu Nat.
Kdy se dvě hodnoty typu
A přesně tak to zapíšeme. Nejprve musíme zmínit, co vlastně děláme. Vkládáme typ instance Eq NatDoplníme definici rovnosti dvou prvků typu Nat podle výše uvedeného rozboru.
instance Eq Nat
where Zero == Zero = True
Succ x == Succ y = x == y
_ == _ = False
kde v klauzuli Succ x == Succ y = x == y je == na pravé straně rekurzivně volaná ta samá funkce, neboť x i y jsou opět typu Nat, čili můžou být pouze ve tvaru Zero nebo Succ x.
A to je celé. Nyní můžeme hodnoty typu
Aby mohl být typ v typové třídě
|