Haskell Hero

Jak jsme si ukázali v lekci Typy I, v Haskellu máme k dispozici krabičku všech celých čísel, krabičku všech znaků nebo třeba krabičku dvou logických hodnot. Někdy je výhodné vytvořit si novou krabičku a do ní nasypat hodnoty, se kterými chceme pracovat.

Příklad

Vytvořte datový typ, který bude obsahovat všechny čtverce zadané délkou strany a všechny obdélníky zadané délkou své výšky a šířky. Délku vyjádřete celým číslem.

Pojmenujme si náš nový datový typ například Obrazec. Pozor na velké počáteční 'O'!

Například čtverec o délce strany 4 bude vypadat Ctverec 4, čtverec o délce strany 10 bude vypadat Ctverec 10, atd. Pozor na velké počáteční 'C'!

Obdélník šířky 7 a délky 2 bude vypadat 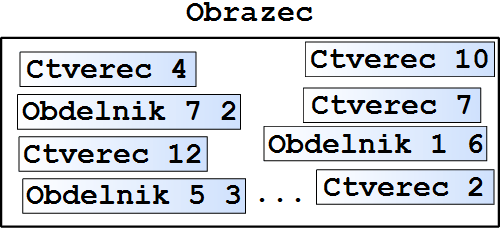Obdelnik 7 2, obdélník šířky 1 a výšky 6 bude vypadat Obdelnik 1 6, atd.

Obecně chceme vytvořit krabičku Obrazec ve které budou všechny hodnoty ve tvaru Ctverec Integer a Obdelnik Integer Integer. Což zapíšeme následovně:

data Obrazec = Ctverec Integer | Obdelnik Integer Integer

Poznámka: Pokud bychom chtěli pracovat s obrazci, které nebudou mít celočíselné rozměry, místo typu Integer použijeme Float nebo Double.

Umíme tedy definovat datový typ Obrazec, který obsahuje všechny čtverce ve tvaru Ctverec Integer a všechny obdélníky ve tvaru Obdelnik Integer Integer, kde za Integer můžeme dosadit libovolné celé číslo.

Mohli bychom například vytvořit datový typ Slovnik definovaný následovně:

data Slovnik  =  Slovo String

Zde můžeme String nahradit libovolným řetězcem. Tento datový typ obsahuje například hodnoty:

Slovo "Ahoj"
Slovo "Haskell"
Slovo "@{&#Đđ÷"

Pracujeme s novými krabičkami

Nyní, když máme vytvořenou krabičku všech čtverců a obdélníků, s ní můžeme začít pracovat jako s každým jiným datovým typem.

Příklad

Definujte funkce obvod a obsah, které budou počítat obvod a obsah hodnot typu Obrazec.

Nejdříve ze všeho musíme uvést naši definici datového typu Obrazec.

data Obrazec = Ctverec Integer | Obdelnik Integer Integer

Obě funkce budou typu Obrazec -> Integer, takže si rovnou nadepíšeme typové anotace:

obvod :: Obrazec -> Integer
obsah :: Obrazec -> Integer

A teď již k samotným definicím. Už ze základní školy víme, že obvod čtverce, který má délku strany x se rovná 4 * x. A přesně to samé napíšeme:

obvod            :: Obrazec -> Integer
obvod (Ctverec x) = 4 * x

Pozor na závorky! V typové anotaci uvádíme, že funkce obvod má být unární, což znamená, že si bere jeden argument. Pokud bychom napsali

obvod Ctverec x = 4 * x

Hugs by funkci obvod přiřadil jako parametr datový konstruktor Ctverec a proměnnou x. Přitom funkce obvod očekává, že dostane jednu hodnotu typu Obrazec.

Tuto definici můžeme hned doplnit i na obvod obdélníka. Víme totiž, že obvod obdélníka šířky x a výšky y se rovná 2 * (x + y).

obvod               :: Obrazec -> Integer
obvod (Ctverec x)    = 4 * x
obvod (Obdelnik x y) = 2 * (x + y)

Obdobně zadefinujeme funkci obsah:

obsah               :: Obrazec -> Integer
obsah (Ctverec x)    = x ^ 2
obsah (Obdelnik x y) = x * y

Když se s takto zadefinovanými funkcemi zeptáme Hugse, jaký je obvod obdélníka 5 × 3, bude nám správně sděleno, že 16.

   obvod (Obdelnik 5 3)
~> 2 * (5 + 3)
~> 2 * 8
~> 16

Rekurzivní datové typy

Nyní jsme v situaci, kdy umíme zadefinovat jednoduchý datový typ. Někdy se ale může stát, že budeme potřebovat definovat typ složitější. Například bychom chtěli vytvořit datový typ Nat znázorňující přirozená čísla s nulou ve tvaru Zero, což je nula, nebo Succ x, což je následník (z angl. successor) čísla x, kde x je typu Nat. Jinými slovy vytvořit krabičku, která by obsahovala například následující hodnoty:

Zero
  -- nula
Succ Zero
  -- následník nuly - jedna
Succ (Succ Zero)
  -- následník následníka nuly - dva
Succ (Succ (Succ Zero))
  -- následník následníka následníka nuly - tři
...

Jak takový typ zadefinovat? Musíme popsat všechny jeho hodnoty. V příkladu z předchozího odstavce byly hodnoty typu Obrazec buďto Ctverec Integer nebo Obdelnik Integer Integer, kde za Integer můžeme dosadit libovolné celé číslo. Zde máme takové tvary dva:

Zero
Succ Nat

Kde za Nat můžeme rekurzivně dosadit libovolnou hodnotu typu Nat. Typ Nat tedy můžeme definovat následovně:

data Nat  =  Zero  |  Succ Nat

Takto definovaný datový typ pouze udává strukturu uložení dat v paměti. Není řečeno, jak se mají jeho hodnoty v případě potřeby vypisovat na obrazovku. Nejjednodušší způsob, jak vypisování zprovoznit, je doplnit definici datového typu o řetězec deriving Show. Pozor na malé 'd' a velké 'S'!. Definice typu Nat s umožněným vypisováním na obrazovku tedy bude vypadat následovně:

data Nat  =  Zero  |  Succ Nat  deriving Show

Funkce nad rekurzivními typy

Zde si zadefinujeme jednoduchou funkci nad typem Nat z předchozího odstavce. Pro lepší pochopení je u každého kroku uvedena analogie se sčítáním jablek.

Příklad

Jablka	`Nat`
Definujte funkci `plusJablka`, které dáme jako argumenty dvě nádoby s jablky a ona nám vrátí nádobu, ve které bude tolik jablek, jako ve dvou vstupních nádobách dohromady.	Definujte funkci `plusNat :: Nat -> Nat -> Nat`, která bude sčítat dvě čísla typu `Nat`.

Čím začít? Uvědomme si, co můžeme s hodnotami typu Nat podle naší definice dělat. Můžeme pouze zjistit, zda je hodnota tvaru Zero, nebo Succ (...). Nic víc. To znamená, že do funkce plusNat nám může jako první argument vstoupit buďto Zero, nebo Succ (...). Jak se v jednotlivých situacích zachovat?

V prvním argumentu je prázdná nádoba. Můžeme říct, že v obou nádobách je dohromady stejně jablek jako v nádobě druhé. Výsledkem je tedy druhá nádoba.	Vyhodnocujeme výraz `plusNat Zero y`. Chceme, aby výsledkem sčítání hodnoty `Zero` s hodnotou `y` byla hodnota `y`. Výraz tedy vyhodnotíme na `y`.
V prvním argumentu je nádoba s alespoň jedním jablkem. Jablko přehodíme do nádoby druhé a znovu zkusíme, jestli už je první nádoba prázdná.	Vyhodnocujeme výraz `plusNat (Succ x) y`. A to na výraz `plusNat x (Succ y)`, čímž číslo v prvním argumentu o jedničku zmenšíme a číslo ve druhém od jedničku zvětšíme.
Jelikož je v první nádobě jen konečně mnoho jablek, víme, že první nádoba se jednou musí úplně vyprázdnit.	Jelikož číslo v prvním argumentu je pouze konečně velké a při každém vyhodnocení podle této větve se o jedničku zmenší, nastane chvíle, kdy se zmenší na nulu.
Přeskládali jsme všechna jablka z první nádoby do druhé a jako výsledek vzali druhou nádobu.	Postupným zmenšováním prvního argumentu a současným zvětšováním druhého argumentu jsme v prvním argumentu dosáhli nuly a v tuto chvíli vyhodnotili výraz na druhý argument.

Funkci plusNat tedy můžeme definovat následovně:

plusNat            ::  Nat -> Nat -> Nat
plusNat  Zero    y  =  y
plusNat (Succ x) y  =  plusNat x (Succ y)

<= Vstup a výstup I předchozí lekce následující lekce Funkce na seznamech II =>